Research

My research is primarily focused on classical general relativity and its observational implications.

Regular black holes

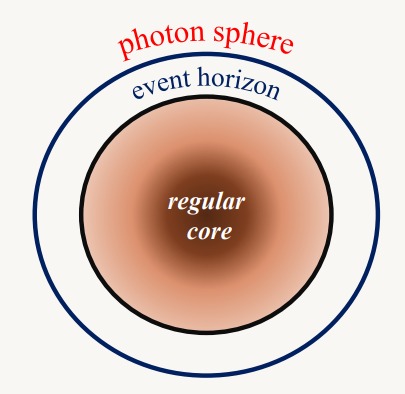The resolution of spacetime singularities, which arise in the gravitational collapse of initially stable structures, is a fundamental challenge in general relativity. Regular black holes provide a promising framework for addressing this issue, replacing the singularity of vacuum black holes in Einstein’s theory with a regular core. The figure illustrates a typical static, spherically symmetric, regular black hole. Our research focuses on developing innovative models of regular black holes and investigating their physical properties, including their stability, thermodynamics, and observational signatures.

Black hole shadow

The intense gravitational field of a black hole bends and traps light, resulting in the formation of a shadow—a dark silhouette surrounded by photon rings. The geometry and parameters of a black hole determine the shape and size of its shadow. Photons with low angular momentum are scattered away, while those with high angular momentum fall into the black hole, creating the characteristic dark region. Our research investigates the shadows of various regular black hole spacetimes, including both rotating and non-rotating configurations, to understand their distinct observational features and potential detectability.

Nonlinear electrodynamics

In classical Maxwell electrodynamics, the electric field and self-energy of a point charge diverge as the radial distance approaches zero. This issue can be resolved by introducing nonlinear modifications to Maxwell’s Lagrangian, resulting in finite self-energy for point charges. Our work investigates the extent to which nonlinear electrodynamics can eliminate spacetime singularities. By coupling these Lagrangians with general relativity, we aim to identify non-singular spacetime solutions and study their physical and mathematical properties.